Indifferenzkurven

Indifferenzkurven (oder auch Isonutzenkurven oder Isonutzenlinien) sind eine grafische Darstellung von allen Gütermengenkombinationen, bei denen der Haushalt nach seinen Präferenzen indifferent ist. Dabei versteht man unter indifferent, dass er also alle gleich gut einschätzt.

Die Darstellung von Indifferenzkurven folgt immer nach den selben Schema. Auf der horizontalen Achse eines Koordinatensystems wird die Menge des Konsums an Gut 2 aufgetragen, während auf der vertikalen Achse die Menge des Konsums an Gut 1 dargestellt wird. Die eigentliche Kurve ergibt sich dann durch das Auftragen von Punkten unter der Annahme, dass beide Güter unendlich teilbar sind.

Eine normale Indifferenzkurve zeigt nicht an, welches welches Güterbündel bevorzugt wird. Deswegen findet man bei manchen Indifferenzkurven auch manchmal entsprechende Pfeile vor.

In der Regel gelten bei Indifferenzkurven folgende vier Annahmen:

• Nichtsättigung
• Stetigkeit
• Transitivität
• Konvexität

Eine wichtige Eigenschaft von Indifferenzkurven ist die Tatsache, dass sich Indifferenzkurve nie schneiden! Das rührt unter anderem von der Transitivität her. Nehmen wir beispielsweise die drei Güterbündel X, Y und Z. In diesem Fall müsste Z auf der Indifferenzkurve von A, als auch auf der Indifferenzkurve von B liegen. Damit gilt, dass der Konsument zwischen A und Z (A ∼ Z), wie auch zwischen B und Z (B ∼ Z) indifferent ist. Zieht man nun das Transivitätsaxiom heran, dann muss auch gelten, dass X zu Y (X ∼ Y) indifferent ist. Die ist aber nicht der Fall, da X und Y auf zwei verschiedenen Indifferenzkurven liegen und es gilt A 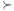B

Spezielle Indifferenzkurven

Es gibt spezielle Indifferenzkurven, bei denen man mit einem Blick sieht, um was es sich dabei handelt. Diese werden nachfolgend dargestellt:

Perfekte Substitute

Bei perfekten Substituten sind die Indifferenzkurven linear und berühren die Achsen. Dies Güter werden so genannt, weil man sie gegeneinander austauschen (substituieren) kann. Das wäre beispielsweise der Fall bei Butter oder Margarine. Manche Menschen unterscheiden in diesem Fall nicht, sodass es ihnen egal ist ob sie Butter oder Margarine auf ihr Brot streichen, Hauptsache eins von beiden. Die Indifferenzkurven der perfekte Substitute zeichnen sich durch eine konstante negative Steigung aus.

Perfekte Komplemente

Bei den perfekten Komplementen sehen die Indifferenzkurven L-förmig aus. Unter perfekten Komplementen versteht man Güter, die nur in Kombination miteinander sinnvoll verwendet werden können Ein gutes Beispiel ist dabei ein Paar Schuhe, das aus einem linken und einen rechten Schuh besteht. Es bringt einem nichts, wenn man zwei linke und einen rechten Schuh hat, da man mit dem überzähligen linken Schuh nichts anfangen kann. Daher kommt auch die L-Form der Indifferenzkurven.

Bads/Ungüter

Wie der englische Begriff schon sagt, ist ein Ungut bzw. ein "bad" ein Gut, das der Konsument nicht mag. Dementsprechend schaut ein Haushalt darauf, dass er so wenig wie möglich von diesen entsprechenden "Gütern" hat.

Neutrale Güter

Ein Gut ist dann neutral, wenn es den Konsument nicht kümmert, wie viel er davon hat. Bei neutralen Gütern sind die Indifferenzkurven vertikale Linien.

Sättigung

Bei der Sättigung kreisen die Indifferenzkurven in Elipsenform um einen sogenannten Sättigungspunkt. Ein schönes Beispiel für das Sättigungsphänomen ist der Bier- und Fernsehkonsum eines Abends.